Category: General mathematics

Variations On Approximation – An Exploration in Calculation

Mary Pat Campbell

Link: https://www.soa.org/news-and-publications/newsletters/compact/2014/january/com-2014-iss50/variations-on-approximation–an-exploration-in-calculation/

Graphic:

Excerpt:

Before we get into the different approaches, why should you care about knowing multiple ways to calculate a distribution when we have a perfectly good symbolic formula that tells us the probability exactly?

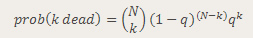
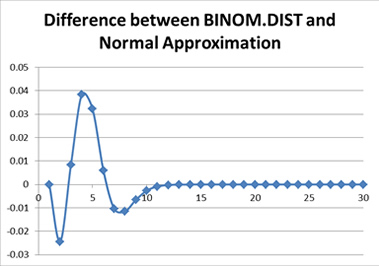
As we shall soon see, having that formula gives us the illusion that we have the “exact” answer. We actually have to calculate the elements within. If you try calculating the binomial coefficients up front, you will notice they get very large, just as those powers of q get very small. In a system using floating point arithmetic, as Excel does, we may run into trouble with either underflow or overflow. Obviously, I picked a situation that would create just such troubles, by picking a somewhat large number of people and a somewhat low probability of death.

I am making no assumptions as to the specific use of the full distribution being made. It may be that one is attempting to calculate Value at Risk or Conditional Tail Expectation values. It may be that one is constructing stress scenarios. Most of the places where the following approximations fail are areas that are not necessarily of concern to actuaries, in general. In the following I will look at how each approximation behaves, and why one might choose that approach compared to others.

Author(s): Mary Pat Campbell

Publication Date: January 2014

Publication Site: CompAct, SOA

What is the value of the p-value?

Mary Pat Campbell

Link: https://www.lucymcgowan.com/talk/north_carolina_translational_and_clinical_sciences_institute/

Slides: https://docs.google.com/presentation/d/1W51xBJOG7C37vHLJuBR4WT6NCJXQN0Iah-NKk9VCLxg/edit#slide=id.g12240d9f43a_0_0

Graphic:

Abstract:

The debate over the value and interpretation of p-value has endured since the time of its inception nearly 100 years ago. The use and interpretation of p-values vary by a host of factors, especially by discipline. These differences have proven to be a barrier when developing and implementing boundary-crossing clinical and translational science. The purpose of this panel discussion is to discuss misconceptions, debates, and alternatives to the p-value.

Author(s): Lucy D’Agostino McGowan

Publication Date: 26 April 2022

Publication Site: LucymcGowan.com

THE DARTH VADER RULE

Mary Pat Campbell

Link:https://www.sav.sk/journals/uploads/1030150905-M-O-W.pdf

doi: : 10.2478/v10127-012-0025

Graphic:

Excerpt:

In life insurance mathematics, the concept of a survival function is commonly
used in life expectancy calculations. The survival function of a random variable X
is defined at x as the probability that X is greater than a specific value x. For
a non-negative random variable whose expected value exists, the expected value
equals the integral of the survival function. We propose to designate this result
as the Darth Vader Rule1. It holds for any type of random variable, although its
most general form relies on the integration by parts formula for the Lebesgue-
-Stieltjes integral, fully developed by H e w i t t [3]. This result, while known (and
stated in F e l l e r [1]), is not widely disseminated except in life insurance mathematics texts; but it is worth knowing and popularizing because it provides an
efficient tool for calculation of expected value, and gives insight into a property
common to all types of random variables.
We give a proof of the Darth Vader Rule which works for all random variables which are non-negative almost surely and whose expected value exists.
The proof is based not on the Lebesgue integral formulation of [3], but on the
generalized Riemann integration of H e n s t o c k and K u r z w e i l [2], [4]. Since
every Lebesgue integrable function is also generalized Riemann integrable, the
proof here includes all cases covered by [3].
While the result is simple to state and comprehend, its proof using Lebesgue
integral theory is somewhat complex.

Author(s): Pat Muldowney — Krzysztof Ostaszewski — Wojciech Wojdowski

Publication Date: 2012

Publication Site: Tatra Mountains Mathematical Publications

Fermat’s Library – Japanese Banking Numerals

Mary Pat Campbell

Link: https://www.linkedin.com/posts/fermatslibrary_japanese-contains-a-separate-set-of-numerals-activity-6888483726783717376-O8n4

Graphic:

Excerpt:

Japanese contains a separate set of numerals used in legal and financial documents to curb fraud by preventing someone from adding strokes to previously written numbers (e.g. turning a 1 into a 2, or changing 3 to a 5).

Author(s): Fermat’s Library

Publication Date: 17 Jan 2022

Publication Site: LinkedIn

Taylor Heinicke Was Solving Differential Equations. Then the NFL Called.

Mary Pat Campbell

Link:https://www.wsj.com/articles/taylor-heinicke-washington-football-team-math-engineering-old-dominion-11632328555

Excerpt:

Last December, a student in professor Fang Hu’s partial differential equations class at Old Dominion University reached out with a problem Hu had never experienced in decades of academia. His pupil said he had just been offered a high-profile job, starting immediately, and might need some special accommodation to finish his course work.

“I got called by an NFL team,” Taylor Heinicke told Hu. “I’m going to be very, very busy.”

“I was like seriously? Really? Professional football?” Hu says. “‘He really takes this course very seriously,’ was my first reaction.”

Heinicke had bounced around the fringes of the NFL for years, but by last year he had bounced out so far that he went back to school to finish his degree. Then, in the span of a month, Heinicke went from taking the highest-level undergraduate mathematics courses at Old Dominion to playing quarterback for the Washington Football Team. He started a playoff game in which he nearly outdueled Tom Brady.

….

When Heinicke was the school’s quarterback from 2011 to 2014, he rewrote record books. He owns the all-time mark for most passing completions in a season in FCS history, and he even broke the record for all of Division I with 730 passing yards in a single game. (That was later surpassed by two quarterbacks. One of them was Patrick Mahomes.)

Heinicke’s success on the field at ODU was boosted by the same traits that led him to take engineering and math classes. His coaches found that their quarterback was both talented and capable of understanding things on a football field that other quarterbacks simply couldn’t.

…..

Just days after Washington’s season ended, Hu heard again from his student. Heinicke finally had time to turn in his final exam.

Author(s): Andrew Beaton

Publication Date: 23 Sept 2021

Publication Site: WSJ

Have Fun With Approximations!

Mary Pat Campbell

Link: https://www.linkedin.com/pulse/have-fun-approximations-mary-pat-campbell/

Graphic:

Pdf: https://drive.google.com/file/d/0ByabEDuWaN6FNmZhTDBYeEVrNVE/view?resourcekey=0-U4GI2_9zn4UQdWza1bq95w

Excerpt:

In the pre-computer days, people used these approximations due to having to do all calculations by hand or with the help of tables. Of course, many approximations are done by computers themselves — the way computers calculate functions such as sine() and exp() involves approaches like Taylor series expansions.

The specific approximation techniques I try (1 “exact” and 6 different approximation… including the final ones where I put approximations within approximations just because I can) are not important. But the concept that you should know how to try out and test approximation approaches in case you need them is important for those doing numerical computing.

Author(s): Mary Pat Campbell

Publication Date: 3 February 2016 (updated for links 2021)

Publication Site: LinkedIn, CompAct, Society of Actuaries

John Napier : Mirifici Logarithmorum Canonis Descriptio….. & Constructio…..

Mary Pat Campbell

Link: http://www.17centurymaths.com/contents/napiercontents.html

Graphic:

Excerpt:

A modern translation with some notes of Napier’s Descriptio, with the Latin version presented last, is presented here. Book I is an introduction to the new science of logarithms; while Book II is devoted to a thorough explanation of the solution of plane and spherical triangles. The original work was translated by Edward Wright in 1616 and both the original and the translation were used by Briggs at Gresham College as part of the education of navigators, for whom the work was intended; astronomers also benefited. This work and its sequel the Constructioshould be read before Briggs’s Arithmetica is approached. I present here a spreadsheet derivation of Napier’s Log Tables : there was a ‘slippery mistake’ in one of the tables of the Constructio, which together with the rounding that took place, limited the original tables accuracy to only perhaps 5 places ; thus, there cannot be complete agreement with the original tables.. The Constructio in which Napier promised to elaborate on his method then follows; though Napier did not live long enough to see this work in print. This work is the first time the exponential function appears in mathematics, under the guise of a geometric number line. This is a brilliant exercise in lateral thinking to solve an apparently unsolvable problem : the time and labour spent in long calculations. I am much indebted to the translation of this work by William Macdonald (1888) , that has helped me to unravel some of the knots in Napier’s Latin and saved much time. An appendix is also given; and one should also mention the existence of another book that was printed before the death of the philosopher, his Rabdologea, in which Napier’s other calculating devices that include his bones and promptuary are set out. As an excellent translation by William Frank Richardson has been published in the history of computing series, there is no need to expound on this here. Perhaps I should say that an internet friend of mine, Jim Hanson, has resurrected the Promptuary, and you should visit his website if you want to know how to make one :

Translated text: http://www.17centurymaths.com/contents/napier/ademonstratiobookone.pdf

Author(s): John Napier (original in Latin), translated by Ian Bruce

Publication Date: 30 April 2012

Publication Site: 17th century maths

MathHistory: A course in the History of Mathematics

Mary Pat Campbell

Link: https://www.youtube.com/playlist?list=PL55C7C83781CF4316

Video example:

Description:

Starting with the ancient Greeks, we discuss Arab, Chinese and Hindu developments, polynomial equations and algebra, analytic and projective geometry, calculus and infinite series, Stevin’s decimal system, number theory, mechanics and curves, complex numbers and algebra, differential geometry, topology, the origins of group theory, hyperbolic geometry and more. Meant for a broad audience, not necessarily mathematics majors.

Author(s): N.J. Wildberger

Publication Date: 3 March 2020 [last time list updated]

Publication Site: Insights into Mathematics at YouTube