Link:https://www.sav.sk/journals/uploads/1030150905-M-O-W.pdf
doi: : 10.2478/v10127-012-0025
Graphic:
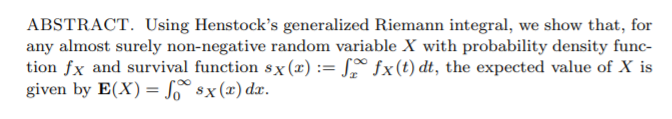
Excerpt:
In life insurance mathematics, the concept of a survival function is commonly
used in life expectancy calculations. The survival function of a random variable X
is defined at x as the probability that X is greater than a specific value x. For
a non-negative random variable whose expected value exists, the expected value
equals the integral of the survival function. We propose to designate this result
as the Darth Vader Rule1. It holds for any type of random variable, although its
most general form relies on the integration by parts formula for the Lebesgue-
-Stieltjes integral, fully developed by H e w i t t [3]. This result, while known (and
stated in F e l l e r [1]), is not widely disseminated except in life insurance mathematics texts; but it is worth knowing and popularizing because it provides an
efficient tool for calculation of expected value, and gives insight into a property
common to all types of random variables.
We give a proof of the Darth Vader Rule which works for all random variables which are non-negative almost surely and whose expected value exists.
The proof is based not on the Lebesgue integral formulation of [3], but on the
generalized Riemann integration of H e n s t o c k and K u r z w e i l [2], [4]. Since
every Lebesgue integrable function is also generalized Riemann integrable, the
proof here includes all cases covered by [3].
While the result is simple to state and comprehend, its proof using Lebesgue
integral theory is somewhat complex.
Author(s): Pat Muldowney — Krzysztof Ostaszewski — Wojciech Wojdowski
Publication Date: 2012
Publication Site: Tatra Mountains Mathematical Publications